1. 博弈

1.1 前提

双人博弈：博弈对象只有己方和对方，没有第三方
二人零和：若一方获胜取得x分，则另一方失败取得-x分
全信息：博弈过程中，任何一方都完全了解当前格局和过去历史，不存在信息差
非偶然：任何一方都只能根据当前实际情况来采取行动，不存在“碰运气”的行为
利益完全对立：任何一方动作的目的都只能是击败对方，不存在暂时合作
交替行动：每方一次只能进行一次动作，接着就轮到对方做动作

1.2 博弈树

根结点：博弈的初始状态
叶子结点：博弈的终止状态
边：可能的行动
效益值：每个终止状态对一方的有利程度和对另一方的不利程度
估值函数e(p)：根据当前状态p和博弈规则，给出当前结点p的效益值
深度：计算当前状态的效益值所需要向下参考的子树层数

2. 极大极小分析法

零和：若己方的效益值为x则对方的效益值为-x，因此只需考虑其中一方的的效益值

倒推法：自底向上，根据子结点的效益值确定父结点的效益值，且叶子结点的效益值是已知的

博弈目的：若将己方作为根结点要获胜，则己方每次选择都要追求最大的效益值，而对方每次选择都要追求最小的效益值

MAX结点：==己方做选择的层的全部结点，总是选择效益值最大的子结点–>对己方最有利（极大的含义）==
MIN结点 ：==对方做选择的层的全部结点，总是选择效益值最小的子结点–>对己方最不利（极小的含义）==

3. α-β剪枝

3.1 基本概念

极大极小算法的局限性：必须算出全部子结点结点的效益值才能判断父节点的效益值

极大极小算法的优化：及时剪掉无用的子结点分枝，仅根据部分子结点就可以得到父节点的效益值

MAX结点：

  • α值：MAX结点的子结点的最大值
  • β值：MAX结点的左边/已遍历兄弟结点的最小值

MIN结点：

  • α值：MIN结点的左边/已遍历兄弟结点的最大值
  • β值：MIN结点的子结点的最小值

3.2 α剪枝–删除以MAX结点为根结点的分支

剪枝原理：MAX结点选择最大值，但MAX结点的父结点是MIN结点要选择最小值，如果存在α>β即该MAX结点最终取值一定≥α，因此MIN结点会暂时选择β分支，而不会考虑α分支（所以才叫α-cuts）

3.3 β剪枝–删除以MIN结点为根结点的分支

剪枝原理：MIN结点选择最小值，但MIN结点的父结点是MAX结点要选择最大值，如果存在α>β即该MIN结点最终取值一定≤β，因此MAX结点会暂时选择α分支，而不会考虑β分支（所以才叫β-cuts）

4. α-β剪枝算法分析

4.1 算法的操作（重点）

  • 初始化：令根节点的α=-∞，β=+∞
  • 传递（从上往下）：==将父结点α值和β值都赋给子结点==
  • 回溯（从下往上）：==父MAX结点的α值 = 子MIN结点的β值，父MIN结点的β值 = 子MAX结点的α值==
  • 剪枝（从左往右）：==如果结点更新后的α≥β，则剪去以该结点为根结点的分支==

4.2 操作的理解（赋值原理）

  • 回溯的单一赋值：MAX的β值与子结点无关，MIN的α值与子结点无关

  • 回溯的交叉赋值：

    • 父MAX的α值取决于子MIN，子MIN根据β取值
    • 父MIN的β值取决于子MAX，子MAX根据α取值

  • 传递的对应赋值：

    • MAX的子结点最大值 = 子结点已遍历兄弟结点的最大值 --> 父MAX结点的α值与子MIN结点的α值是相同的
    • MIN的子结点最小值 = 子结点已遍历兄弟结点的最小值 --> 父MIN结点的β值与子MAX结点MAX的β值是相同的

  • 虽然MAX和MIN结点的α值和β值的意义不一样，但是观察发现上述α-cut和β-cut的前提都是α≥β

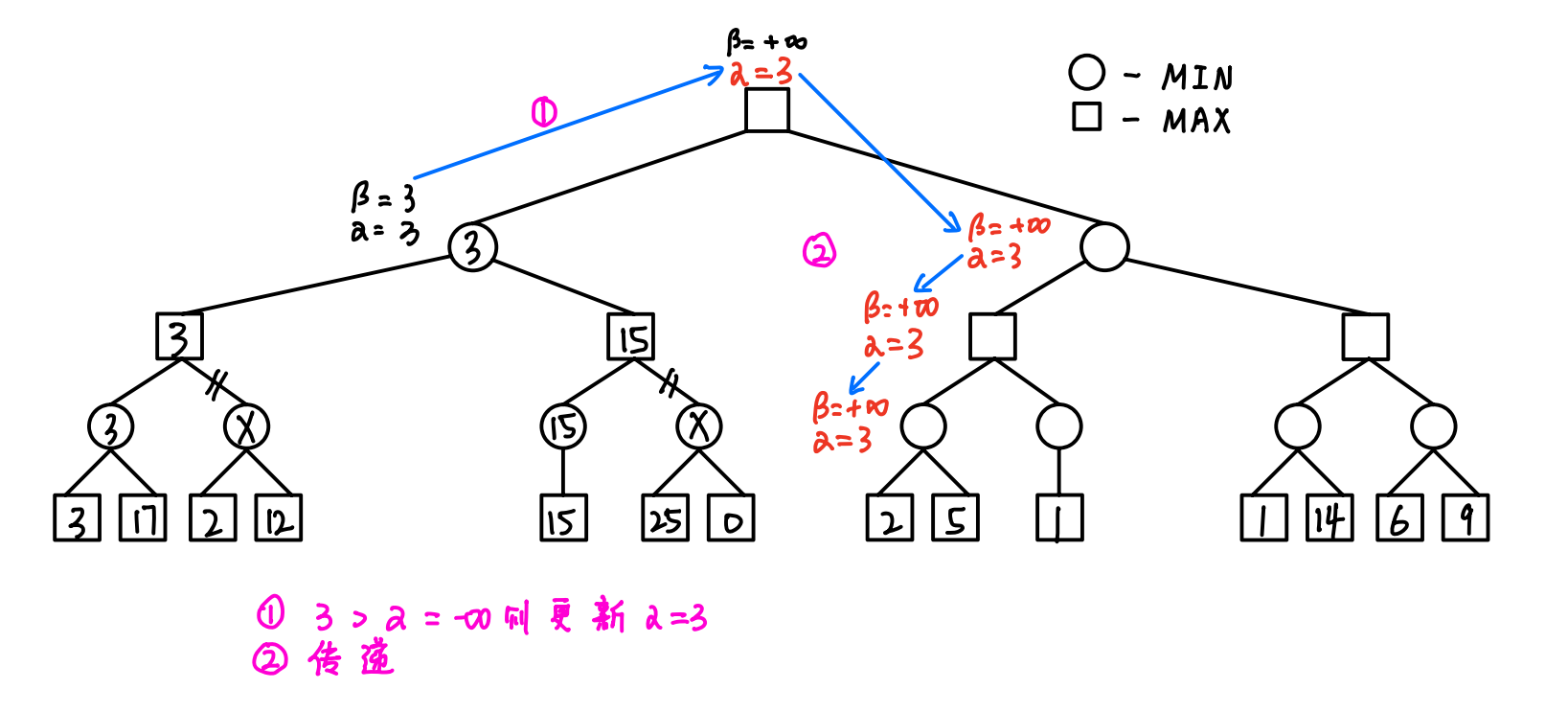
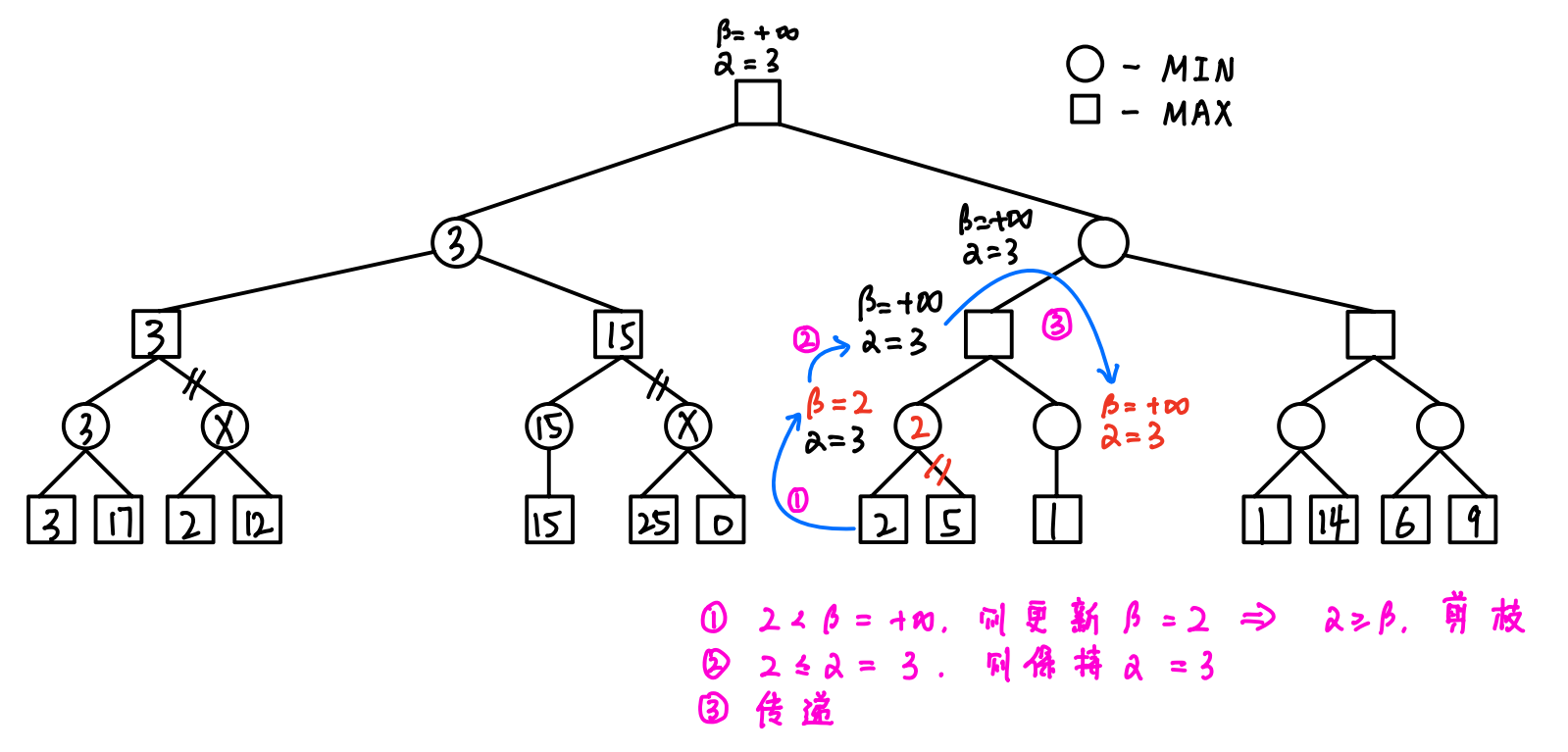
4.3 算法的流程（详细图解）

  1. 令根结点的α = +∞，β = -∞，然后逐渐向下传递，直到遇到第一个叶子结点
  2. 反复进行以下三步：
    • 传递：根据父结点更新子结点 -> 成对对应赋值
    • 回溯：根据子结点更新父结点 -> 单一交叉赋值
    • 剪枝：一旦出现α ≥ β的情况，及时剪枝
  3. 得到根结点的效益值，并选择对应的子结点作为下一次扩展的根结点









4.4 伪代码

5. α-β算法的通用代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Node:
    # 初始化数据成员
    def __init__(self,state,side):
        self.state = state      # 当前状态
        self.next = None        # 目标状态
    # 获取当前状态的全部子状态
    def get_substates(self,nextside):
        pass
    # 获取当前节点对应状态的目标价值
    def evaluate(self):
        pass
    # 检查是否是最佳状态或最坏状态
    def check(self):
        pass

def alpha_beta_cut(node:Node,alpha,beta,turn,depth,max_depth):
    flag = node.check()
    if flag == 最佳状态:
        return float('inf')
    elif flag == 最坏状态:
        return float('-inf')
    elif flag == 持平状态:
        return 0
    elif depth == max_depth:
        return node.evaluate()
    
    if turn == 'MAX':
        node_alpha,node_beta = alpha,beta
        for substate in node.get_substates(turn):
            subnode = Node(substate)
            value = alpha_beta_cut(subnode,node_alpha,node_beta,'MIN',depth+1,max_depth)
            if node_alpha < value:
                node_alpha = value
                node.next = substate
            if node_alpha >= node_beta:
                break
        return node_alpha

    if turn == 'MIN':
        node_alpha,node_beta = alpha,beta
        for substate in node.get_substates(turn):
            subnode = Node(substate)
            value = alpha_beta_cut(subnode,node_alpha,node_beta,'MAX',depth+1,max_depth)
            if node_beta > value:
                node_beta = value
                node.next = substate
            if node_alpha >= node_beta:
                break
        return node_beta

initial_state = [初始状态]
root = Node(initial_state)
nextstep = alpha_beta_cut(root,float('-inf'),float('inf'),'MAX',0,3)

6. 效率分析

令分支系数=b（即一个结点的平均子结点个数）；搜索树深度=d

  • 极大极小过程的时间复杂度：O(bd)
  • α-β过程的时间复杂度：O(bd/2)–>在相同代价下，α-β过程是极大极小过程向前看的走步数的两倍

搜索效率与选取的α、β值和最终倒退值的相似度有关，如果α值和β值的选取越接近最终倒退值，剪掉的分支就越多，搜索效率越高

7. 井字棋

移步另一篇文章